Q.1
Correct Answer is:C
Solution Explain:
Q.2
Correct Answer is:C
Solution Explain:
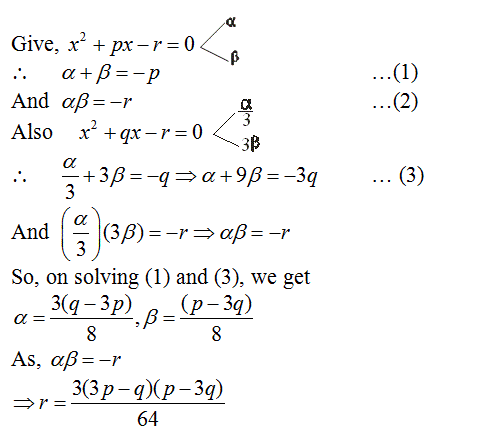
Q.3
Correct Answer is:D
Solution Explain:
Q.4
Correct Answer is:C
Solution Explain:
Q.5
Correct Answer is:A
Solution Explain:
Q.6
Correct Answer is:C
Solution Explain:
Q.7
Correct Answer is:A
Solution Explain:
Q.8
Correct Answer is:C
Solution Explain:
Q.9
Correct Answer is:C
Solution Explain:
Q.10
Correct Answer is:B
Solution Explain:
Q.11
Correct Answer is:A
Solution Explain:
Q.12
Correct Answer is:B
Solution Explain:
Q.13
Correct Answer is:C
Solution Explain:
Q.14
Correct Answer is:A
Solution Explain:
Q.15
Correct Answer is:B
Solution Explain:
Q.16
Correct Answer is:B
Solution Explain:
Q.17
Correct Answer is:C
Solution Explain:
Q.18
Correct Answer is:B
Solution Explain:
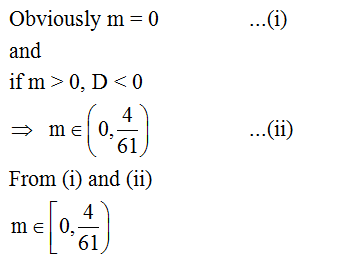
Q.19
Correct Answer is:B
Solution Explain:
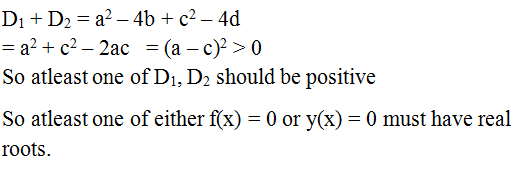
Q.20
Correct Answer is:D
Solution Explain:
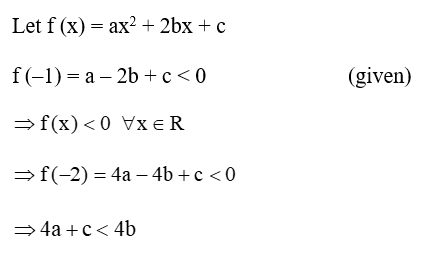
Q.21
Correct Answer is:A
Solution Explain:
Q.22
Correct Answer is:B
Solution Explain:
Q.23
Correct Answer is:B
Solution Explain:
Q.24
Correct Answer is:B
Solution Explain:
Q.25
Correct Answer is:C
Solution Explain:
Q.26
Correct Answer is:A
Solution Explain:
Q.27
Correct Answer is:C
Solution Explain:
Q.28
Correct Answer is:A
Solution Explain:
Q.29
Correct Answer is:B
Solution Explain:

Q.30
Correct Answer is:C
Solution Explain:
Q.31
Correct Answer is:C
Solution Explain:
Q.32
Correct Answer is:C
Solution Explain:
Q.33
Correct Answer is:C
Solution Explain:

Q.34
Correct Answer is:D
Solution Explain:
Q.35
Correct Answer is:B
Solution Explain:
Q.36
Correct Answer is:D
Solution Explain:
Since, p(x) = 0 is a quadratic equation with real coefficients having purely imaginary roots
Therefore p(x) = ax2 + b where a and b are of same sign
Now p(p(x)) = 0 ⇒ a(ax2 + b)2 + b = 0
But if x is purely real or purely imaginary then x2 is purely real
So, (ax2 + b)2 is purely real and greater than or equal to zero
⇒ p(p(x)) = a(ax2 + b)2 + b can never be zero
[as a and b are of same sign and b ≠ 0]
⇒ p(p(x)) = 0 can have only complex roots
Q.37
Correct Answer is:C
Solution Explain:
Q.38
Correct Answer is:B
Solution Explain:
Q.39
Correct Answer is:D
Solution Explain:
Q.40
Correct Answer is:A
