Q.1
Solution Explain:
Q.2
Solution Explain:
f(0)=r is odd. Let r = 2n +1,n ∈ I
f(-1) = -1 + p- q+ 2n + 1= p - q+ 2n is odd
⇒ exactly one of p,q is odd
f(1) = 1 + p + q+ 2n + 1= p + q+ 2n + 2 is odd
If possible suppose α,β,γ ∈ I be zeros of f(x).
⇒ x3+px2+qx+r=x3-(α+β+γ)x2+(αβ+βγ+γα)x-αβγ
⇒r=-αβγ ⇒ α,β,γ are odd integers
⇒ p =-(α+β+γ) is odd and q=αβ + βγ + γα is also odd.
It is a contradiction. Hence f(x)=0 cannot have three integer roots.
Q.3
Solution Explain:
Q.4
Solution Explain:
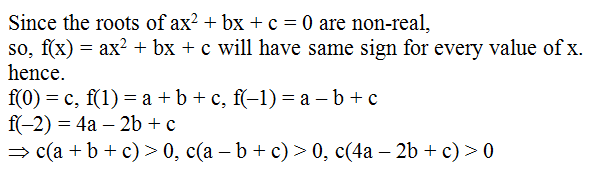
Q.5
Solution Explain:

Q.6
Solution Explain:
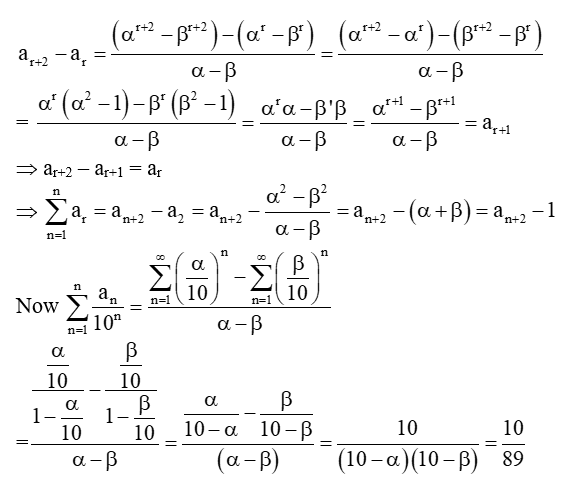
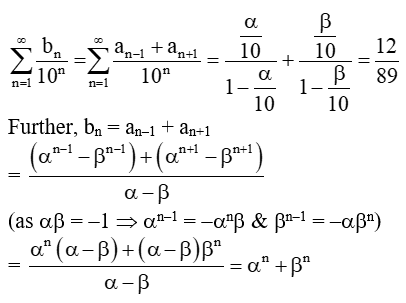
Q.7
Solution Explain:
According to condition 1,-1 lies inside the roots of the equation x2 + (3a - a2) x- 3a3 = 0
f(1) < 0
1 + 3a - a2 - 3a3 < 0
(a - 1)(a +1) (3a+ 1) > 0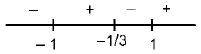
a ∈ (-1, -1/3) ∪ (1, ∞).....(i)
f(-1) < 0
1 - 3a + a2 - 3a3 < 0
(a2 + 1) (3a - 1) > 0
a ∈ (1/3, ∞) ....(ii)
From (i) ∩ (ii)
a ∈ (1, ∞)
Q.8
Solution Explain:
D = (b2 + c2 - a2)2 - 4b2c2
D = (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
D= [(b-c)2 - a2][(b + c)2 - a2]
D = (b - c + a)(b - c - a)(b + c + a)(b + c - a)
D = -(a + b - c)(c + a - b)(b + c - a)(b + c + a) < 0 (as sum of two sides > third side of Δ)
⇒ D < 0 and parabola is upward
Hence f(x) > 0 ∀ x ∈ R
Q.9
Solution Explain:
2q = p + r
q2-4pr ≥ 0
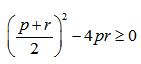

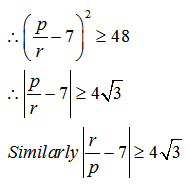
Q.10
Solution Explain:
Q.11
Solution Explain:
Q.12
Solution Explain:
Let f (x) = ax2 + bx + c
Its discriminant D = b2 – 4ac < 0
and f(–1) = a – b + c > 0
So, f (x) > 0 for all x ∈ R
So, a > 0
f (0) > 0 ⇒ c > 0
f (1) > 0 ⇒ a + b + c > 0
f(–2) > 0 ⇒ 4a – 2b + c > 0 .
