Permutation and Combination - Algebra -Integer Type Questions(JEE ADVANCED) Part 2

 Q.1

Correct Answer is: [14]  

Solution Explain:

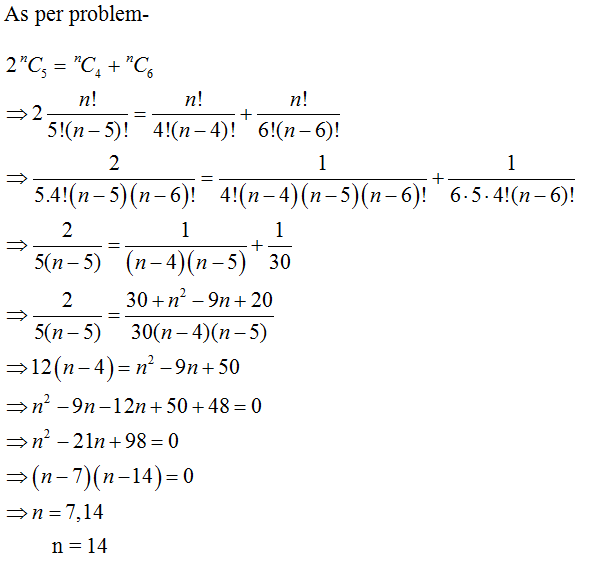
Q.2

Correct Answer is: [20]  

Solution Explain:

Q.3

Correct Answer is: [1]  

Solution Explain:

The last digit  of powers of 3  will be 3,9,7,1 and it repeats in the same order. The last digit of powers of 7 will be 7,9,3,1 and it repeats in same order. Now 3m +7n will be multiple of 10 as 3+7, 9+1, 7+3,1+9
⇒ (m,n) will be of the form (4t+1, 4k +1),(4t+2,4k) (4t+3,4k+3) and (4t,4k+2)
So total number of ways = 5×5+5×5+5×5+5×5=100

Q.4

Correct Answer is: [31650]  

Solution Explain:

Q.5

Correct Answer is: [5]  

Solution Explain:

Q.6

Correct Answer is: [135]  

Solution Explain:

Q.7

Correct Answer is: [374]  

Solution Explain:

Q.8

Correct Answer is: [946]  

Solution Explain:

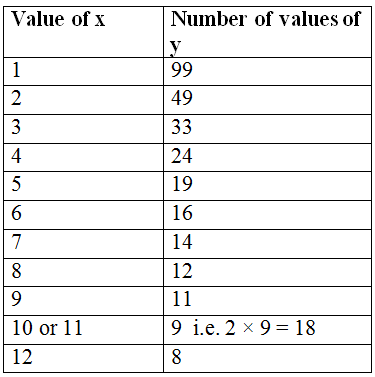
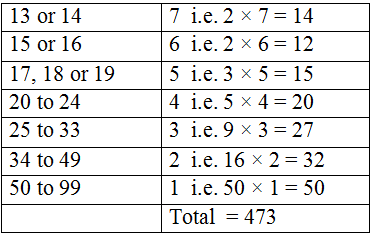
Q.9

Correct Answer is: [512]  

Solution Explain:

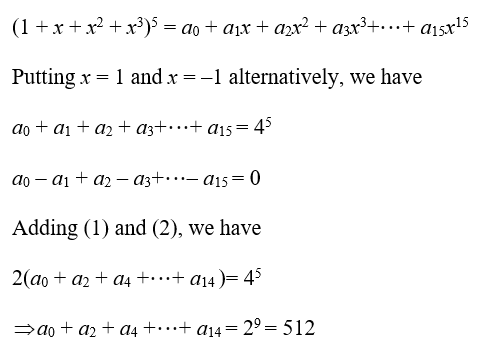
Q.10

Correct Answer is: [5]  

Solution Explain:

Q.11

Correct Answer is: [5]  

Solution Explain:

Q.12

Correct Answer is: [52]  

Solution Explain:

Q.13

Correct Answer is: [54]  

Solution Explain:

Q.14

Correct Answer is: [5]  

Solution Explain:

210 can be factorised as 210 = 2 × 3 × 5 × 7.
All the factors are prime. Clearly any number can be assigned to xi’s in 4 ways. Hence total ways of assigning the factors to xi’s are 44. Now for a particular positive integral solution, we have 4C2 solutions when any two xi’s become negative, and all the four solutions can be negative in 4C4 ways. Hence total number of integral solutions = 44(1+ 4C2 + 4C4) = 8.44.

Q.15

Correct Answer is: [91]  

Solution Explain:

Q.16

Correct Answer is: [41]  

Solution Explain:

Q.17

Correct Answer is: [69]  

Solution Explain:

Q.18

Correct Answer is: [420]  

Solution Explain:

Q.19

Correct Answer is: [10]  

Solution Explain:

Q.20

Correct Answer is: [8]  

Solution Explain: