Q.1
Solution Explain:
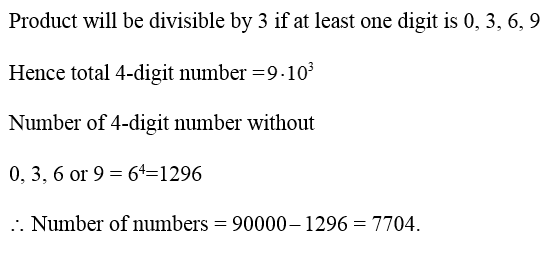
Q.2
Solution Explain:
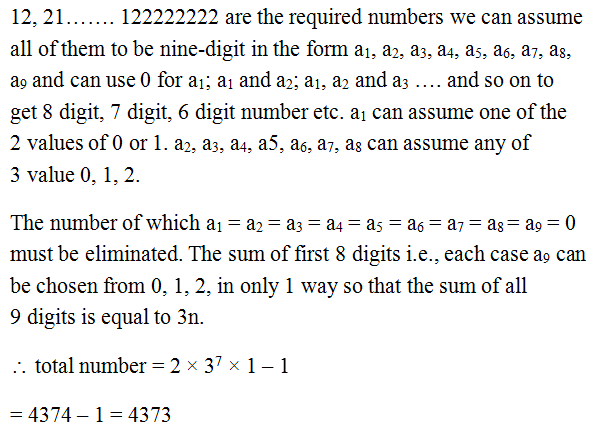
Q.3
Solution Explain:
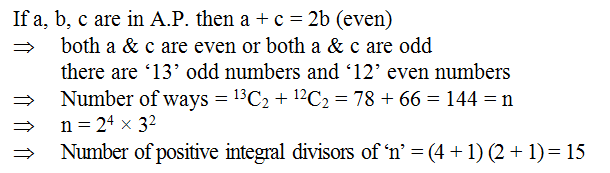
Q.4
Solution Explain:
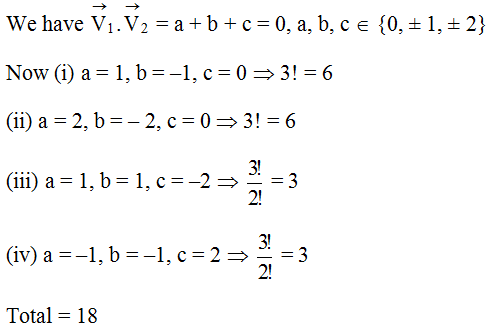
Q.5
Solution Explain:
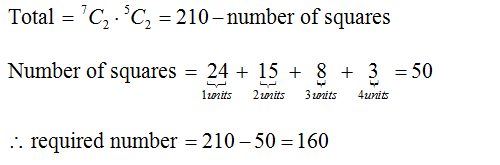
Q.6
Solution Explain:
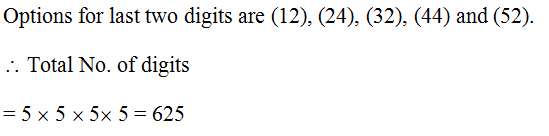
Q.7
Solution Explain:
First 6 distinct digits can be selected in 10C6 ways. Now the position of smallest digit in them is fixed i.e position 4. Of the remaning 5 digits, 2 can be selected in 5C2 ways. These two digits can be placed to the right of 4th position in one way only. The remaning three digits to the left of 4th position are in the required order automatically. So n(S) = 10C6 × 5C2 = 210 × 10 =2100
Q.8
Solution Explain:
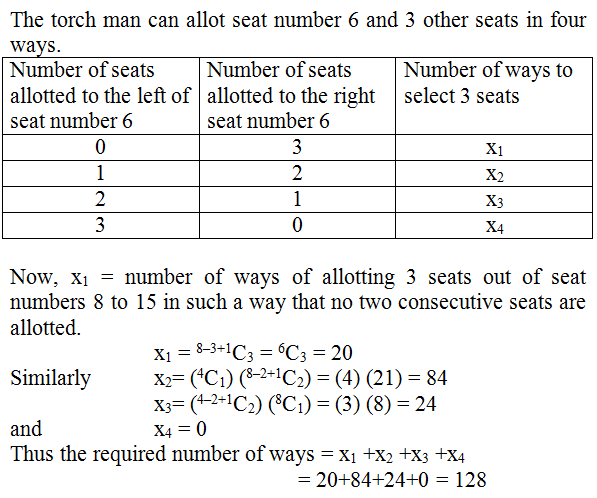
Q.9
Solution Explain:
Q.10
Solution Explain:
Q.11
Solution Explain:
Q.12
Solution Explain:
7!= 24×32 ×5×7
Since the factor should be odd as well as of the form 3t + 1, the factor cannot be a multiple of either 2 or 3. So the factors may be1,5,7 and 35 of which only 1 and 7 are of the from 3t + 1 whose sum is 8
Q.13
Solution Explain:

Q.14
Solution Explain:
Here x1 x2 x3 = 22 × 3 ×5. Let number of twos given to each of x1 x2 x3 be a, b,c. Then a+b+c=2, a,b,c ≥ 0
The number of integral solutions of this equations is equal to coefficent of X2 in (1-x)-3 i e 4C2 i.e the available 2 twos can be distributed among x1 x2 x3 in 3C2 = 3 ways (=coefficent of X in (1-x)-3)
∴ Total number of ways = 4C2 × 3C2 × 3C2 = 6 ×3×3 =54 ways
Q.15
Solution Explain:

Q.16
Solution Explain:

Q.17
Solution Explain:
Q.18
Solution Explain:
Q.19
Solution Explain:

Q.20
Solution Explain:
If three numbers are in G.P., then their exponent must be in A.P.
If a, b, c are selected number in G.P., then the exponents of a and c both are either odd or both even, or otherwise exponent b will not be integer.
Now two odd exponent (from 1, 2, 3, …, 10) can be selected in 5C2 ways and two even exponent can be selected in 5C2 ways.
Hence number of G.P.’s are 25C2 = 20
Q.21
Solution Explain:

Q.22
Solution Explain:
Q.23
Solution Explain:
Q.24
Solution Explain:
Q.25
Solution Explain:
Q.26
Solution Explain:

Q.27
Solution Explain:
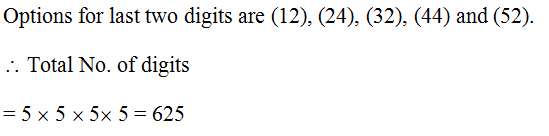
Q.28
Solution Explain:
Q.29
Solution Explain:
Q.30
Solution Explain:
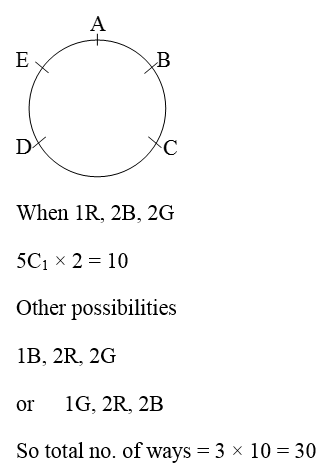
Q.31
Solution Explain:
Let two particular boys as one boy, we have only four boys.
∴5 boys can be seated at a round table when two particular boys are always together = 3! 2!
⇒ 4 girls have are 4 places
∴ 4 girls can be arranged in 4! ways
∴ Required number = 3! 2! 4! = 6. 2. 24
= 288
Q.32
Solution Explain:
Sum of the digits in the tens place
= (4 – 1)! (4 + 5 + 6 + 7)
= 6 × 22
= 132
Q.33
Solution Explain:
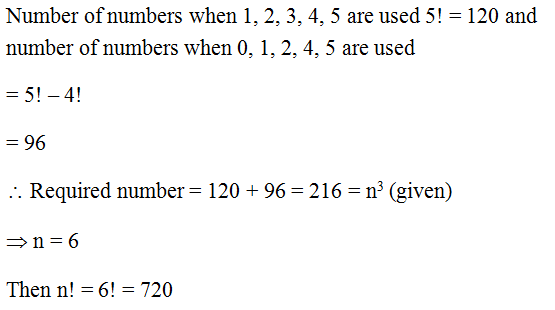
Q.34
Solution Explain:

Q.35
Solution Explain:

Q.36
Solution Explain:
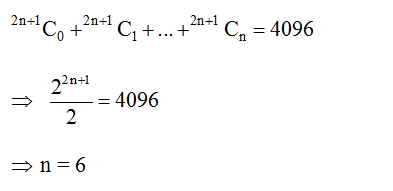
Q.37
Solution Explain:
21,22,23,.........,k-1,k
A.M =21+k/2, G.M = √(21.k)
⇒ k=21 λ2, λ∈I also 100 ≤ k ≤ 999 and k should be odd
⇒ 100/21 ≤ λ2 ≤ 999/21 ⇒ 4.76 ≤ λ2 ≤ 47.57⇒ λ =3,4,5,6 but λ should be odd ⇒ odd λ =3,5 ⇒ 'k' can assume2 different values
Q.38
Solution Explain:

Q.39
Solution Explain:
Q.40
Solution Explain:
3630 = 2 × 3× 5 ×112
Now a divisor will be of the form (4n+1) if divisor is form the help of (4n+1) type number or by (4n+3) types number taken even times.
Hence divisors are 1,5,3 ×11, 112,5 ×3 × 11. i e, 6
