Q.1
Solution Explain:
(mn)!/(m!)n is the number of ways of distributing mn distinct objects in n persons equally.
Hence (mn)!/(m!)n is an integer ⇒ (m!)n |(mn)!.
Similarly (n!)m |(mn)!.
Further m + n <2 m ≤ mn⇒ (m+n)! | (mn)! and m-n < m < mn
⇒ (m-n)! | (mn)!
Q.2
Solution Explain:
f(n) = 1! +2!+3!+...........+n!
f(n+1) = 1! +2!+3!+...........+(n+1)!
f(n+2) = 1! +2!+3!+...........+(n+2)!
f(n+2) - f(n+1) =(n+2)!=(n+2)(n+1)!=(n+2)[f(n+1)-f(n)]
⇒f(n+2)=(n+3)f(n+1)-(n+2)f(n)⇒ P(x)=x+3,Q(x)=-X-2
Q.3
Solution Explain:
Q.4
Solution Explain:
When z = n +1, we can choose x, y from {1, 2, ...., n}. Thus, when z = n + 1, x, y can be chosen in n2. when z = n, x, y can
be chosen in (n – 1)2ways and so on. Thus, there are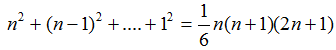
ways of choosing the requisite triplets
Alternatively, triplets with x=y < z, x < y < z, y < x < z
can be chosen in n+1C2, n+1C3, n+1C3 ways.
∴ n+1C2 + 2(n+1C3) = n+2C3 + n+1C3
= 2(n+2C3 ) - n+1C2 ways.
Q.5
Solution Explain:
let the chosen integers be X1 and X2
let there be a integer before X1,b integer between X1 and X2 and c integer after x2
∴ a+b+c=98 where a ≥ 0, b ≥ 10, C ≥ 0
Now if we consider the choices where diffrence is at least 11 then the number of solution is 88+3-1 C3-1=90C2
∴ Number of ways in which b is less than 10 is 100C2-90C2 which is equal to (A)(B) and (C) option
