Q.1
Correct Answer is:A,D
Solution Explain:
Q.2
Correct Answer is:A,B,C,D
Solution Explain:

Q.3
Correct Answer is:A,B,D
Solution Explain:
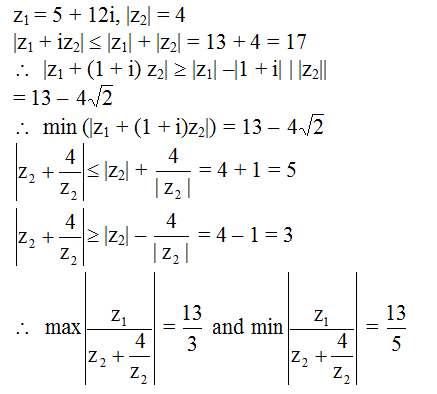
Q.4
Correct Answer is:A,D
Solution Explain:
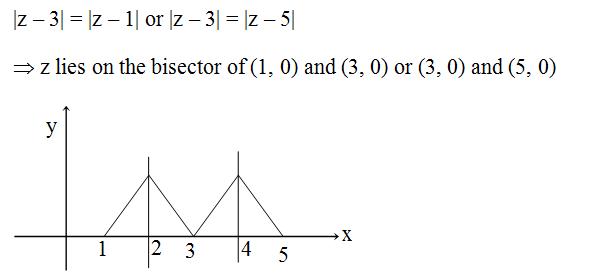
Q.5
Correct Answer is:A,C,D
Solution Explain:
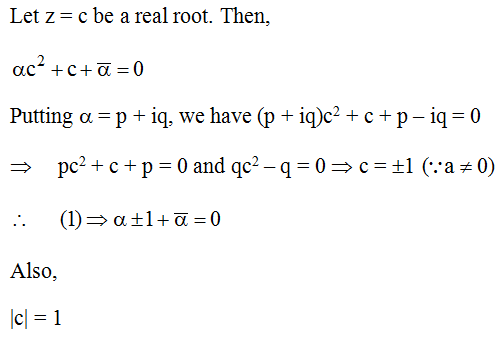
Q.6
Correct Answer is:A,B
Solution Explain:
Q.7
Correct Answer is:A,B,C,D
Solution Explain:

Q.8
Correct Answer is:A,B,D
Solution Explain:

Q.9
Correct Answer is:B,C
Solution Explain:
x4 - 3x2 - 4 = 0 and 2x - 3y + 5 = 0
⇒ (x2 - 4)(x2 +1) = 0 and 2x - 3y +5 = 0
⇒ (x,y) = (2,3) or
Q.10
Correct Answer is:A,B,C,D
Solution Explain:
Q.11
Correct Answer is:A,B,C,D
Solution Explain:
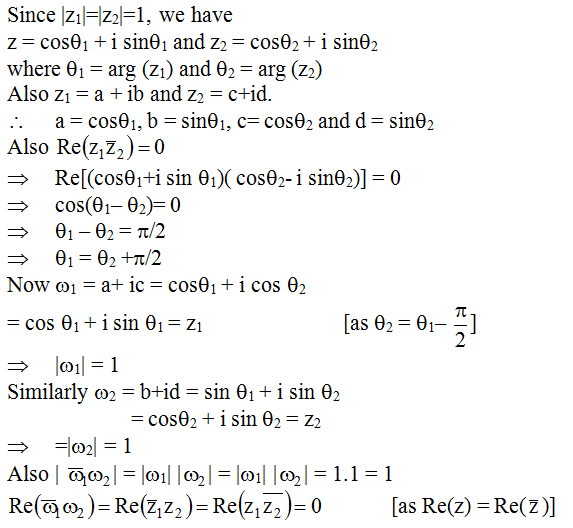
Q.12
Correct Answer is:A,C,D
Solution Explain:
Q.13
Correct Answer is:A,C
Solution Explain:

Q.14
Correct Answer is:A,D
Solution Explain:

Q.15
Correct Answer is:B,C
Solution Explain:
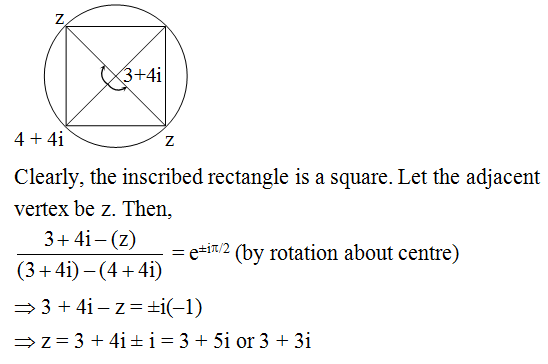
Q.16
Correct Answer is:A,D
Solution Explain:
Q.17
Correct Answer is:C,D
Solution Explain:
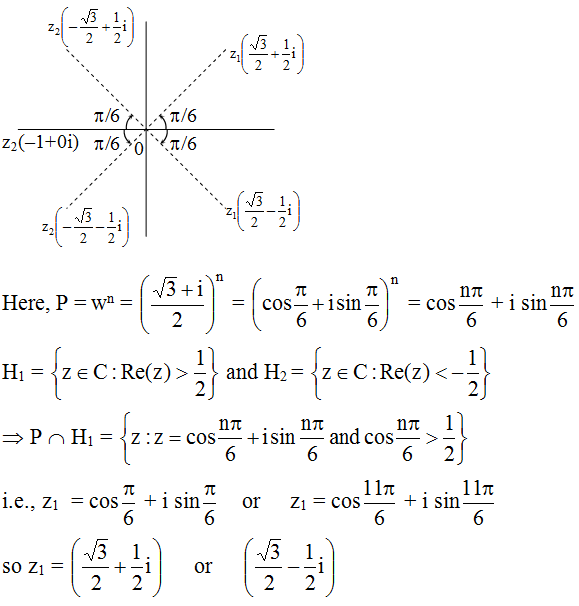

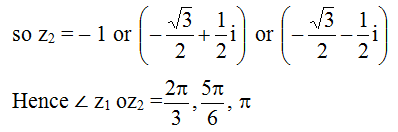
Q.18
Correct Answer is:A,C,D
Solution Explain:

Q.19
Correct Answer is:A,D
Solution Explain:
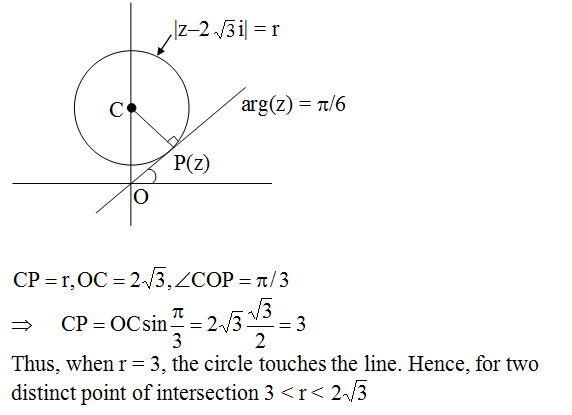
Q.20
Correct Answer is:A,B,C,D
Solution Explain:
Q.21
Correct Answer is:B,C,D
Solution Explain:
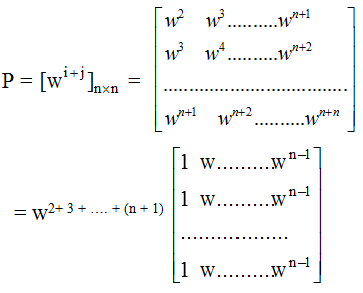

Q.22
Correct Answer is:B,D
Solution Explain:
Q.23
Correct Answer is:B,C
Solution Explain:

Q.24
Correct Answer is:A,B,D
Solution Explain:

Q.25
Correct Answer is:A,B,C,D
Solution Explain:
Q.26
Correct Answer is:A,C,D
Solution Explain:
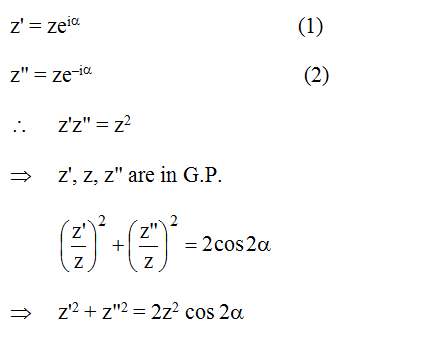
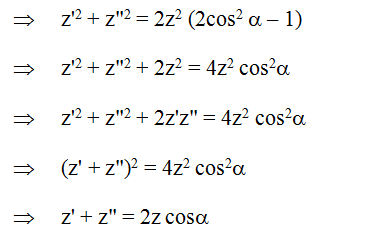
Q.27
Correct Answer is:C,D
Solution Explain:
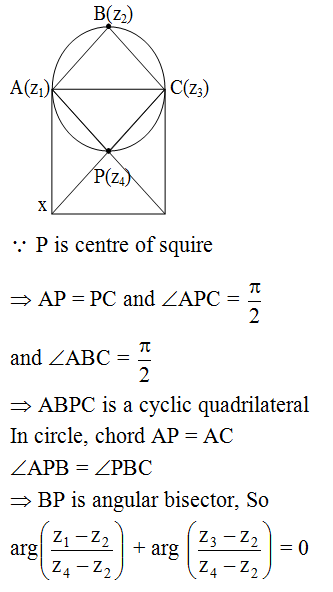
Q.28
Correct Answer is:C,D
Solution Explain:
We have x2 + x + 1 = (x – ω)(x – ω2)
Since f(x) is divisible by x2 + x + 1, f(ω2) = 0, f(ω2) = 0, so
P(ω3) + ωQ(ω3) = 0 ⇒ P(1) + ωQ(1) = 0 …… (1)
P(ω6) + ω2Q(ω6) = 0 ⇒ P(1) + ω2Q(1) = 0 ……. (2)
Solving (1) and (2), we obtain
P(1) = 0 and Q(1) = 0
Therefore, both P(x) and Q(x) are divisible by x – 1. Hence, P(x3) and Q(x3) are divisible by x3 –1 and so by x – 1
Since f(x) = P(x3) + xQ(x3), we get f(x) is divisible by x – 1.
